- Calculul distantei maxime dintre 2 numere prime consecutive

A sti cit mai precis care este distanta maxima dintre 2 nr prime este una din problemele cele mai importante din teoria numerelor prime.

Eu am gasit algoritmul de calcul al acestei probleme.

Fie avem functia numerelor prime 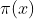$\pi (x)$ . Deasupra acestei functii avem o functie care asimptotic o aproximeaza cit posibil mai mult, aceasta functie o vom numi functia numerelor prime maxim 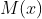$M (x)$ , adica $M (x)\geq \pi (x)$ .

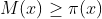Subt functia 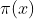$\pi (x)$ avem o functie care asimptotic o aproimeaza cit posibil mai mult, pe aceasta o vom numi functia numerelor prime minim 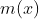$m(x)$ , adica $m(x)\leq \pi (x)$ .

In final $m(x)\leq \pi (x)\leq M(x)$ .

Pot fi anumite cercetari in care anulam egalitatea, dar titlul de functia maxim si functia minim acelasi va ramine 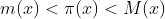$m(x)<\pi (x)<M(x)$ , sau anumite cazuri conjugate.

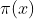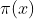In ziua de azi asa o functie care sa intersecteze functia $\pi (x)$ din cite am inteles nu exista, exista o buna aproximare data de Legendre care si ii poarta numele $\pi(n)\leq\left ( \frac{n}{\ln(n)-1.08366} \right ) _{_{n>1. 000.000}}$ , dar aceasta pina la un oarecare numar, care mai apoi sare peste $\pi (x)$ . La fel dupa cum am inteles sub forma de serii si cu anumite constante se poate de determinat functia 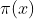$\pi (x)$ . Aceasta este foarte foarte bine, din cauza caci aceste rezultate deja ajuta foarte foarte multe la calculul a o sumedenie de conjecturi, care de risul curcilor au ramas pina azi nerezolvate.

Iata doua functii care aproximeaza functia 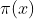$\pi (x)$ din amindoua parti:

$\left ( \frac{x}{ln(x)}\left ( 1+\frac{1}{ln(x)}+\frac{1.8}{ln^{2}(x)}\right ) \right )_{x\geq 32299}\leq \pi (x)\leq \left ( \frac{x}{ln(x)}\left ( 1+\frac{1}{ln(x)}+\frac{2.51}{ln^{2}(x)}\right ) \right )_{x\geq 355991}$

Acum priviti desenul, cine nu intelege desenul si acea egalitate atunci in zadar mai urmareste subiectul.

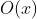Luam un anumit punct $x$ (poate fi si prim si nu) de pe axa $O(x)$ , pe noi ne intereseaza care va fi urmatorul numar la distanta maximala (dependent de $x$ ) care si semnifica distanta maxima dintre doua numere prim, $k$ este aceast numar daca priviti desenul.

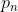- Daca $x$ (sau k) este un nr prim $p_{n}$ si se intimpla caci M(x) (sau m(x))intersecteaza acest punct, iar urmatorul(precedentul) numar prim ar fi la o distanta record de mare, atunci valoarea lui k (lui x)va fi egala cu $p_{n+2}$ (Pn-2) nemijlocit deci intre aceste 2 numere mai exista un numar prim.

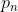- Daca $x$ nu este un nr prim $p_{n}$ atunci intre $x$ si k exista cel putin 2 numere prime.

Valoarea lui $k$ se poate de determinat din egalitatea (o notez pentru importanta ):

$M(x)+1=m(k)$ $(1)$

$k$ - este necunoscuta din aceasta ecuatie, determinarea ei inseamna determinarea distantei maxime dintre 2 numere prime. Cu cit M(x) si m(x) vor aproxima mai bine pe $\pi (x)$ cu atit si o precizie mai buna veti avea.

( Se poate de dermina si scris formula cine este $k$ , dar eu aplic niste notatii personale.

Ecuatia (1) este aceeasi cu: $M(x)+1=m(x)\circ k$

Valoarea lui $k$ deci va fi: $k=(M(x)+1)|\circ m(x)$ )

Sa luam functiile: $\left ( \frac{x}{ln(x)}\left ( 1+\frac{1}{ln(x)}+\frac{1.8}{ln^{2}(x)}\right ) \right )_{x\geq 32299}\leq \pi (x)\leq \left ( \frac{x}{ln(x)}\left ( 1+\frac{1}{ln(x)}+\frac{2.51}{ln^{2}(x)}\right ) \right )_{x\geq 355991}$

Alcatuim deci ecuatia: $\frac{x}{ln(x)}\left ( 1+\frac{1}{ln(x)}+\frac{1.8}{ln^{2}(x)} \right )+1=\frac{k}{ln(k)}\left ( 1+\frac{1}{ln(k)}+\frac{2.51}{ln^{2}(k)} \right )_{x,k\geq 355991}$

Nu e pre potrivita notatiile deoarece noi suntem deprinsi caci x sa fie necunoscuta. Incercam sa prezentam si prin alte notatii:

$p_{n+1}'> p_{n}$ , $p_{n+1}'\approx p_{n}$

Ecuatia deci este:

$M(p_n)+1=m(p'_{n+1})$

Necunoscuta este $p'_{n+1}$ , $p_n$ este o constanta (in notatia cutare un numar prim).

In multe conjecturi in enunt se pune intrebarea daca in un cutare interval exista sau nu numere prime, capetele (unele sau ambele) acestui interval nefiind numere prime, deaceea asa notam:

$M(k)+1=m(\lambda )$

$\lambda$ - fiind necunoscuta, $k$ - constanta ce se cunoaste initial

[cod. Latex| p_{n+1}'> p_{n} | p_{n+1}'\approx p_{n} | M(p_n)+1=m(p'_{n+1}) | M(k)+1=m(\lambda )]

- Mai departe apare problema cum sa calculam aceasta ecuatie.

Functia 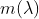$m(\lambda )$ asa arata:

$M(k)+1$ - este o constanta

1. Din metodele de calcul numeric presupun caci metoda tangentelor e mai potrivita de aplicat deoarece ea necesita a sti un capat al intervalului, ceea ce e in cazul nostru. In afara de aceasta pentru cazuri ca acesta atunci cind functia e slab concava/convexa metoda tangentelor si coardelor e foarte potrivita de aplicat (in un numar mic de iteratii ne apropiem foarte rapid de solutie).

Exista totusi o problema, din cauza ca un capat al intervalului e fixat (fie il vom pune valoarea minima de 355991) iar celalalt capat fuge inainte, pentru valori mari ale celuilalt capat calculele tot mai slab aproximeaza.

$M(355991)+1\simeq 300029,216$

- Problema gasirii functiilor M(x) si m(x) cit mai apropiate de 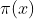$\pi (x)$ este urmatoarea problema dificila.

O posibila varianta de calcul ar fi sa rotim si translam graficile functiilor M1(x) cu 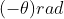$(-\theta) rad$ in punctul 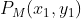$P_{M}(x_{1},y_{1})$ asa incit sa nu incalce 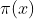$\pi (x)$ si deasemeni sa rotim si translam pe m1(x) in punctul 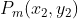$P_{m}(x_{2},y_{2})$ cu $(+\varphi ) rad$ care deasemeni sa nu incalce $\pi (x)$ .

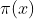- Problema cea mai complicata este aceea caci este totus nevoe de o demonstrare care sa arata caci noile functii rotite sau/si translate pina la o anumita valoare nu vor incalca functia 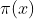$\pi (x)$

Pe calculator putem construi graficele functiilor M(x), 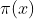$\pi (x)$ , m(x) pentru valori extrem de mari (ordenul sutelor de milioane sau poate si mai mult). Aceste greafice ne vor arata intrucit de mult se abat functiile M(x) si m(x) de functia 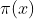$\pi (x)$ . Noi am putea sa facem rotatiile si translatiile "la ochi", dar aceasta necesita totus demonstratii caci nu se va incalca 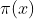$\pi (x)$ , ele cert ca nu vor incalca functia, insa totusi matematica e matematica. Iata ce demonstratie sa facem aceasta e problema nerezolvata la moment.

[Ultima modificare 20.04.16]

Ideas

luni, 7 martie 2016

- Calculul distantei maxime dintre 2 numere prime consecutive

Niciun comentariu:

Trimiteți un comentariu

Arhivă blog