- Conjectura Legendre: Enunt: Intre patratele orecaror doua numere consecutive, exsista cel putin un numar prim.
Rezolvare: Trebue de demonstrat caci intre 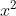 si
si  exista cel putin un numar prim.
exista cel putin un numar prim.
Intrucit limitele intervalului studiat cert nu pot fi numere prime conform "link- distanta max dintre 2 nr. prime" intre aceste intervale exista cel putin 2 numere prime
Intrucit limitele intervalului studiat cert nu pot fi numere prime conform "link- distanta max dintre 2 nr. prime" intre aceste intervale exista cel putin 2 numere prime
Aceasta e simplu in formula  (1) in loc de
(1) in loc de  inlocuim
inlocuim 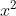 si determinam valoare lui k (fiind solutia ecuatiei).
si determinam valoare lui k (fiind solutia ecuatiei).
Apoi daca exista in acel interval (x^2, (x+1)^2) cel putin 2 numere prime (deoarece capetele nu sunt numere prime), atunci noi va trebui sa lucram nu cu k ci cu k-2.
Apoi daca exista in acel interval (x^2, (x+1)^2) cel putin 2 numere prime (deoarece capetele nu sunt numere prime), atunci noi va trebui sa lucram nu cu k ci cu k-2.
Apoi verificam daca inegalitatea este adevarata (atunci si conjectura e adevarata in caz contrar nu putem spune nimic despre conjectura):
- Conjectura lui Brocard: Enunt: Intre patratele orecaror doua numere prime consecutive, exsista cel putin patru numere prime
Rezolvare: Daca pentru distanta minima dintre cele 2 numere consecutive prime se respecta conjectura, atunci atit mai mult si pentru restul cazurilor.
La fel ca in cazul de mai sus in acest interval exista cel putin 2 numere prime.
La fel ca in cazul de mai sus in acest interval exista cel putin 2 numere prime.
Adica trebue de demonstrat: Caci intre 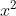 si
si  exista cel putin 4 nr prime. Aceeasi tehnica de rezolvare ca si mai sus:
exista cel putin 4 nr prime. Aceeasi tehnica de rezolvare ca si mai sus:
Rezolvare: Trebue de verificat egalitatea (daca e adevarata, e adevarata conjectura, daca e falsa atunci nu se stie daca e falsa conjectura sau nu):
- Conjectura lui Oppermann: Enunt: Intre 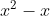 si
si 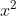 ; la fel intre
; la fel intre 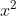 si
si 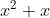 ,
,  , permament exsista cel putin un numar prim.
, permament exsista cel putin un numar prim.
Rezolvare: Trebue de verificat sistemul (daca e adevarat inegalitatile din sistem e adevarata conjectura, daca e falsa atunci nu se stie daca e falsa conjectura sau nu):

- Conjectura lui Andrica: Enunt: Diferența radicalilor a două numere prime consecutive este întotdeauna mai mică decât 1 adica :
Rezolvare: Inegalitatea de mai sus se rezuma la :

Deoarece atunci:
atunci:

Noi ne oprim sa rezolvam:

 - este solutia ecuatiei (1) in functie de
- este solutia ecuatiei (1) in functie de 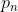 .
.
- Conjectura lui Andrica: Enunt: Diferența radicalilor a două numere prime consecutive este întotdeauna mai mică decât 1 adica :
Rezolvare: Inegalitatea de mai sus se rezuma la :
Deoarece
Noi ne oprim sa rezolvam:
Niciun comentariu:
Trimiteți un comentariu