Ideas: noiembrie 2018

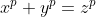
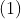
Sa se determine daca ecuatia: $x^{p}+y^{p}=z^{p}$ $(1)$
are solutii intregi pentru: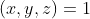 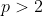$(x,y,z)=1$ , $p>2$ , $p$ - prim

Stim :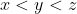 $x< y< z$ ,    Studiem cazurile (asa cazuri mi se pare se poate demonstra caci sunt din start excluse ca posibile sa aiba solutii) :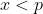   $x<p$

Conform Micii Teoreme a lui Fermat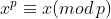    $x^{p}\equiv x(mod\,p)$ aceasta inseamna:

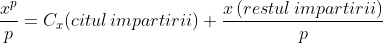
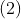
$\frac{x^{p}}{p}=C_{x}(citul\,impartirii)+ \frac{x\,(restul\,impartirii)}{p}$ $(2)$

Daca impartim ecuatia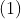 $(1)$ la orice numar (real) atunci ar trebui ca atit partea intreaga cit si fractionara din membrul sting sa fie egal cu membrul drept.

Presupunem caci ecuatia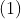 $(1)$ are totus solutii in $N$ si efectuam impartirea:

$\frac{x^{p}}{p}+\frac{y^{p}}{p}=\frac{z^{p}}{p}$

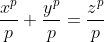
Problema se divide in mai multe cazuri:

Caz 1: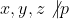    $x,y,z \not| p$
Din ecuatia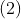 $(2)$ avem:

$C_{x}+\frac{x}{p}+C_{y}+\frac{y}{p}=C_{z}+\frac{z}{p}$    $\Leftrightarrow$    $C_{x+y}+\frac{x+y}{p}=C_{z}+\frac{z}{p}$

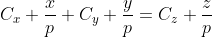
Apare intrebarea daca :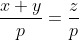 $\frac{x+y}{p}=\frac{z}{p}$ adica daca $x+y=z$ ceea ce este absurd. De aici posibil

rezulta caci presupunerea ca ecuatia (1) are solutii in N e falsa.

Caz 2: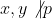 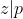$x,y \not| p$ ,    $z|p$ avem:

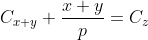$C_{x+y}+ \frac{x+y}{p}=C_{z}$ ca sa aiba o probabilitate minima de adevar egalitatea, ar trebui ca numitorul  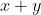 $x+y$ sa fie egal sau multiplu de $p$ . Din conditia x,y nedivizibil cu p conduce la concluzia caci pentru acest cazi ecuatia (1) nu are solutii in N.

Caz 3: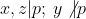 $x,z|p; \,y\not|p$ avem:

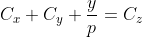$C_{x}+C_{y}+\frac{y}{p}=C_{z}$ => absurditatea existentei solutiilor.

Caz 4: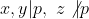      $x,y|p ,\ z\not|p$ avem:

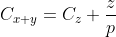$C_{x+y}=C_{z}+\frac{z}{p}$ => absurditatea existentei solutiilor.

Ideas

miercuri, 14 noiembrie 2018

De care triunghiuri sunt mai multe in plan ?!

vineri, 2 noiembrie 2018

Marea Teorema a lui Fermat

Arhivă blog