Ideas: 2018

miercuri, 14 noiembrie 2018

De care triunghiuri sunt mai multe in plan ?!

Ordinea e cam aceasta:

Triunghiuri echilaterale <triunghiuri nule < triunghiuri isoscele < triunghiuri dreptunghice < triunghiuri ascutitunghice < triunghiuri obtuze

vineri, 2 noiembrie 2018

Marea Teorema a lui Fermat

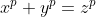
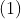
Sa se determine daca ecuatia: $x^{p}+y^{p}=z^{p}$ $(1)$
are solutii intregi pentru: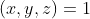 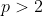$(x,y,z)=1$ , $p>2$ , $p$ - prim

Stim :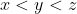 $x< y< z$ ,    Studiem cazurile (asa cazuri mi se pare se poate demonstra caci sunt din start excluse ca posibile sa aiba solutii) :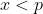   $x<p$

Conform Micii Teoreme a lui Fermat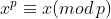    $x^{p}\equiv x(mod\,p)$ aceasta inseamna:

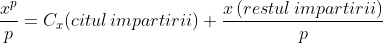
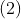
$\frac{x^{p}}{p}=C_{x}(citul\,impartirii)+ \frac{x\,(restul\,impartirii)}{p}$ $(2)$

Daca impartim ecuatia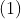 $(1)$ la orice numar (real) atunci ar trebui ca atit partea intreaga cit si fractionara din membrul sting sa fie egal cu membrul drept.

Presupunem caci ecuatia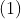 $(1)$ are totus solutii in $N$ si efectuam impartirea:

$\frac{x^{p}}{p}+\frac{y^{p}}{p}=\frac{z^{p}}{p}$

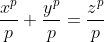
Problema se divide in mai multe cazuri:

Caz 1: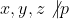    $x,y,z \not| p$
Din ecuatia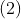 $(2)$ avem:

$C_{x}+\frac{x}{p}+C_{y}+\frac{y}{p}=C_{z}+\frac{z}{p}$    $\Leftrightarrow$    $C_{x+y}+\frac{x+y}{p}=C_{z}+\frac{z}{p}$

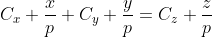
Apare intrebarea daca :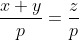 $\frac{x+y}{p}=\frac{z}{p}$ adica daca $x+y=z$ ceea ce este absurd. De aici posibil

rezulta caci presupunerea ca ecuatia (1) are solutii in N e falsa.

Caz 2: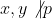 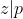$x,y \not| p$ ,    $z|p$ avem:

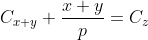$C_{x+y}+ \frac{x+y}{p}=C_{z}$ ca sa aiba o probabilitate minima de adevar egalitatea, ar trebui ca numitorul  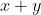 $x+y$ sa fie egal sau multiplu de $p$ . Din conditia x,y nedivizibil cu p conduce la concluzia caci pentru acest cazi ecuatia (1) nu are solutii in N.

Caz 3: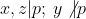 $x,z|p; \,y\not|p$ avem:

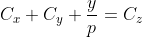$C_{x}+C_{y}+\frac{y}{p}=C_{z}$ => absurditatea existentei solutiilor.

Caz 4: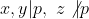      $x,y|p ,\ z\not|p$ avem:

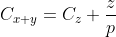$C_{x+y}=C_{z}+\frac{z}{p}$ => absurditatea existentei solutiilor.

duminică, 21 ianuarie 2018

Logica primordiala

Titlul acestui subiect poate nu e prea reusit. In genere aici as dori sa dezbat despre unele lucruri esentialea, de la care se porneste totul, de la origine.

Mi-au aparut o multime de intrebari si observatii la aceasta tema si le voi expune.

- Orice cuvint din o propozitie are un sir finit de explicatii, explicatiile se opresc pina la nedefinitii ( elemente) si conventii. Ex. de nedefinitii (in viziunea mea): punct, infinit, informatie..
Dar si aceste elemente nedefinite sunt relative, deoarece depinde in conceptia cui sunt ele vazut, conform carei conventii sunt ele vazute, eu spre exemplu una inteleg cei acea "informatie", altul poate altfel intelege cei aceasta "informatie".

- Valoarea de adevar a unei axiome (postulat) nu poate fi determinata ca fiind adevarata (A) sau falsa (F). La baza tuturor teoremelor stau axiomele. La baza tuturor teoriilor stau teoremele. La baza tuturor stiintelor stau teoriile. In rezultat tot ceea ce noi stim ca e cert si demonstrat ca fiind foarte adevarat in realitate nu e deloc asa.

- Cum putem demonstra daca o anumita propozitie e axioma sau teorema ?!

- O anumita deomnstratie a anumitei teoreme, probabil mai necesita inca o anumita demonstratie care precizeaza caci demonstratia anterioara se refera la cutarea teorema, dar si aceasta anterioara demonstratie probabil necesita si ea alta demonstratie care sa precizeze ce explica ea, ...

- Teorema lui Godel la fel nu trebuie preamarita, din simplul modiv caci este... teorema, dar la baza teoremelor stau axiomele (din sistemul lor axiomatic), la care nu li se poate de determinat valoarea de adevar.